基尼系数本身反应了样本的不确定度。当基尼系数越小的时候，说明样本之间的差异性小，不确定程度低。

假设 t 为节点, 那么该节点的 GINI 系数的计算公式为:

$$ GINI(t)=1-\sum_k[p(C_k|t)]^2 $$

这里 p(Ck|t) 表示节点 t 属于类别 Ck 的概率, 节点 t 的基尼系数为 1 减去各类别 Ck 概率的平方和

举个例子. 有集合 D, 一共12行记录, 假设基于属性A 将D 划分为两个集合.

• 集合1: 6个都去打篮球
• 集合2: 3个去打篮球, 3个不去

针对集合 1，所有人都去打篮球，所以 p(Ck|t)=1，因此 GINI(t)=1-1=0。

针对集合 2，有一半人去打篮球，而另一半不去打篮球，所以，p(C1|t)=0.5，p(C2|t)=0.5，GINI(t)=1-（0.50.5+0.50.5）=0.5。

通过两个基尼系数你可以看出，集合 1 的基尼系数最小，也证明样本最稳定，而集合 2 的样本不稳定性更大。

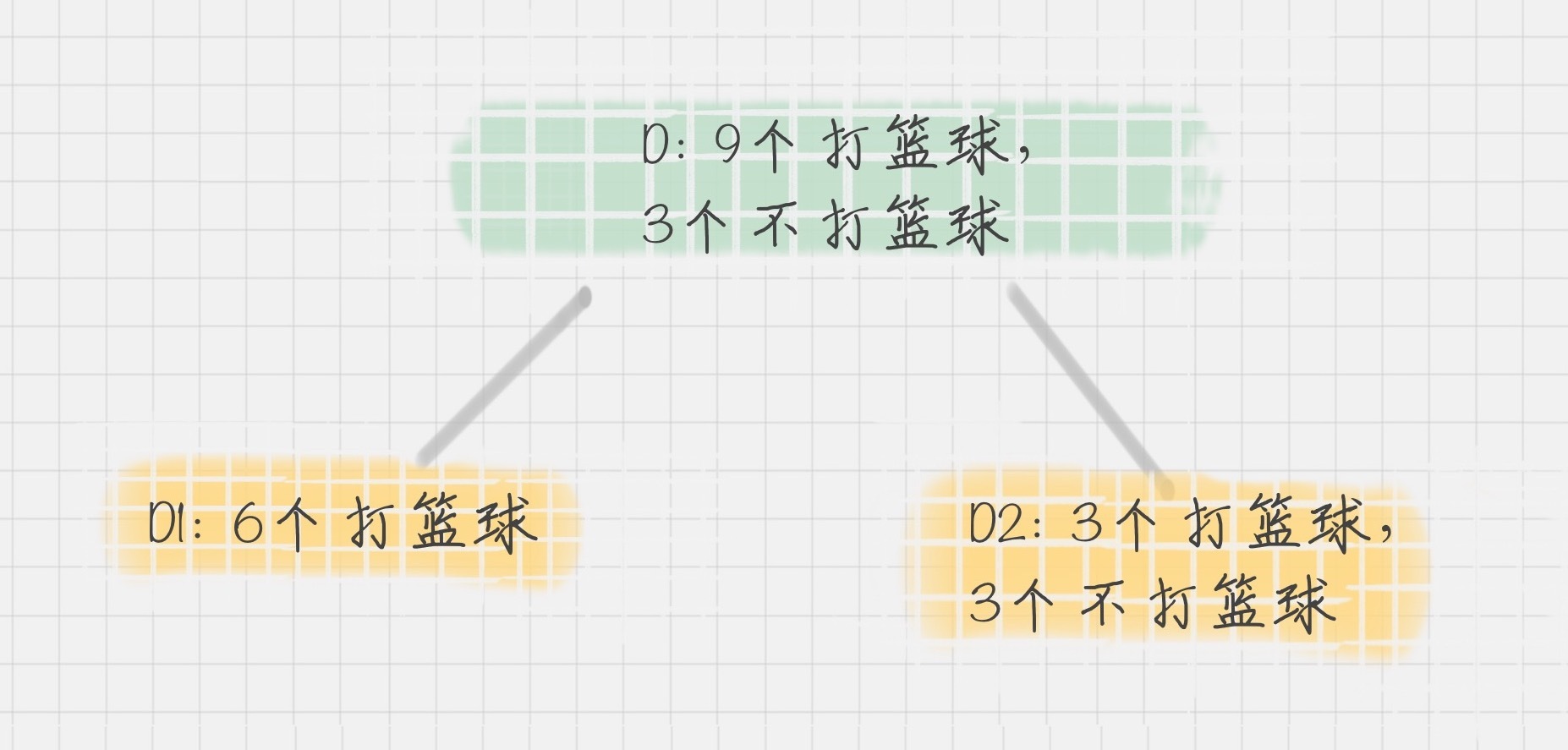
在 CART 算法中，基于基尼系数对特征属性进行二元分裂，假设属性 A 将节点 D 划分成了 D1 和 D2，如下图所示：

节点 D 的基尼系数等于子节点 D1 和 D2 的归一化基尼系数之和，用公式表示为：

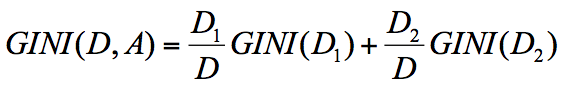
归一化基尼系数代表的是每个子节点的基尼系数乘以该节点占整体父亲节点 D 中的比例。上面我们已经计算了集合 D1 和集合 D2 的 GINI 系数，得到：

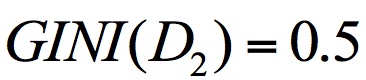
所以节点 D 的基尼系数为：