
Bloom Filter 又称布隆过滤器. 是一种空间效率很高的随机数据结构,它利用位数组很简洁地表示一个集合,并能判断一个元素是否属于这个集合。
Bloom Filter 的这种高效是有一定代价的:在判断一个元素是否属于某个集合时,有可能会把不属于这个集合的元素误认为属于这个集合(false positive)。因此,Bloom Filter 不适合那些 “零错误” 的应用场合。而在能容忍低错误率的应用场合下,Bloom Filter 通过极少的错误换取了存储空间的极大节省。
下面我们具体来看 Bloom Filter 是如何用位数组表示集合的。初始状态时,Bloom Filter 是一个包含 m 位的位数组,每一位都置为 0。

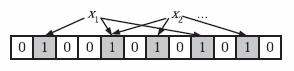
为了表达 S={x1, x2,…,xn} 这样一个 n 个元素的集合,Bloom Filter 使用 k 个相互独立的哈希函数(Hash Function),它们分别将集合中的每个元素映射到 {1,…,m} 的范围中。对任意一个元素 x,第 i 个哈希函数映射的位置 hi(x) 就会被置为 1(1≤i≤k)。注意,如果一个位置多次被置为1,那么只有第一次会起作用,后面几次将没有任何效果。在下图中,k=3,且有两个哈希函数选中同一个位置(从左边数第五位)。
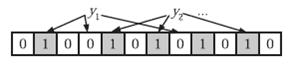
在判断 y 是否属于这个集合时,我们对 y 应用 k 次哈希函数,如果所有 hi(y) 的位置都是 1(1≤i≤k),那么我们就认为 y 是集合中的元素,否则就认为 y 不是集合中的元素。下图中 y1 就不是集合中的元素。y2 或者属于这个集合,或者刚好是一个 false positive。
前面我们已经提到了,Bloom Filter 在判断一个元素是否属于它表示的集合时会有一定的错误率(false positive rate),下面我们就来估计错误率的大小。在估计之前为了简化模型,我们假设 kn<m 且各个哈希函数是完全随机的。当集合 S={x1, x2,…,xn} 的所有元素都被 k 个哈希函数映射到 m 位的位数组中时,这个位数组中某一位还是 0 的概率是:
$$ p' = (1 - \frac{1}{2})^{kn} \approx e^{-kn/m} $$
其中 1/m 表示任意一个哈希函数选中这一位的概率(前提是哈希函数是完全随机的),(1-1/m) 表示哈希一次没有选中这一位的概率。要把 S 完全映射到位数组中,需要做 kn 次哈希。某一位还是 0 意味着 kn 次哈希都没有选中它,因此这个概率就是(1-1/m)的 kn 次方。令 p = e-kn/m 是为了简化运算,这里用到了计算 e 时常用的近似:
$$ \lim_{x\rightarrow\infty} (1 - \frac{1}{x})^{-x} = e $$
令ρ为位数组中 0 的比例,则ρ的数学期望 E(ρ)= p’。在ρ已知的情况下,要求的错误率(false positive rate)为:
$$ (1-\rho)^k \approx (1-p')^k \approx (1-p)^k $$
(1-ρ) 为位数组中 1 的比例,(1-ρ)k 就表示 k 次哈希都刚好选中 1 的区域,即 false positive rate。上式中第二步近似在前面已经提到了,现在来看第一步近似。p’只是ρ的数学期望,在实际中ρ的值有可能偏离它的数学期望值。M. Mitzenmacher 已经证明 [2] ,位数组中 0 的比例非常集中地分布在它的数学期望值的附近。因此,第一步的近似得以成立。分别将 p 和 p’代入上式中,得:
$$ f' = ( 1- (1- \frac{1}{m})^{kn})^{k} = ( 1- p' )^k $$